지금까지 들었던 헷징의 예는 너무 단순화된 것이므로 현실성이 없다. 즉, 헷저는 자산의 매도시기 또는 매입시기를 날짜까지 정확히 알 수 있으며, 자산가격의 변동위험을 거의 완벽하게 제거하는 데 선물계약을 이용할 수 있다고 가정하였다. 실제로 헷징은 그렇게 간단하지 않은데, 그 이유는 아래와 같다.
1. 헷징 대상자산이 선물계약의 기초자산과 정확히 동일하지 않을 수 있다.
2. 헷저가 자산을 매입하거나 매도할 날짜를 정확히 모를 수 있다.
3. 헷저는 만기일 전에 선물계약을 마감해야 할 경우가 있다.
이러한 문제점들이 소위 베이시스위험(basis risk)을 발생시킨다. 베이시스위험에 대해 자세히 설명하기로 하자.
17.1 베이시스
베이시스(basis)는 다음과 같이 정의된다. [붙임] 참조
베이시스 = 헷징 대상자산의 현물가격 - 헷징에 이용된 기초자산의 선물가격
만일 헷징 대상자산과 선물의 기초지산이 같다면, 선물의 만기 시 베이시스는 0이어야 한다. 그리고 만기 전의 베이시스는 양(+) 또는 음(-)양 값을 갖는다. 10. 선물시세표의 [표 10.1]로부터 2010년 5월 26일에 금의 베이시스는 음(-)의 값을 갖고 단기 콩의 베이시스는 양(+)의 값을 갖고 있음을 알 수 있다.
시간이 흐름에 따라 특정월의 현물가격과 선물가격이 동일한 크기로 변하는 것은 아니다. 그 결과 베이시스는 변한다. 베이시스가 증가하는 것을 강세 베이시스(strengthening of the basis)라고 일컫는다. 반대로 베이시스가 감소하는 것을 약제 약세 베이시스(weakening of the basis)라고 일컫는다. [그림 17.1]은 베이시스가 시간에 파라 어떻게 변하는지를 보여주고 있다. 이 예에서 선물계약 만기 전의 베이시스는 양(+)의 값을 갖는다.
아래와 같은 기호를 사용하여 베이시스위험의 본질을 살펴보기로 하자.
S1: t1시점에서의 현물가격
S2: t2시점에서의 현물가격
F1: t1시점에서의 선물가격
F2: t2시점에서의 선물가격
b1: t1시점에서의 베이시스
b2: t2시점에서의 베이시스
| 그림 17.1 시간의 변화에 따른 베이시스의 변화 |
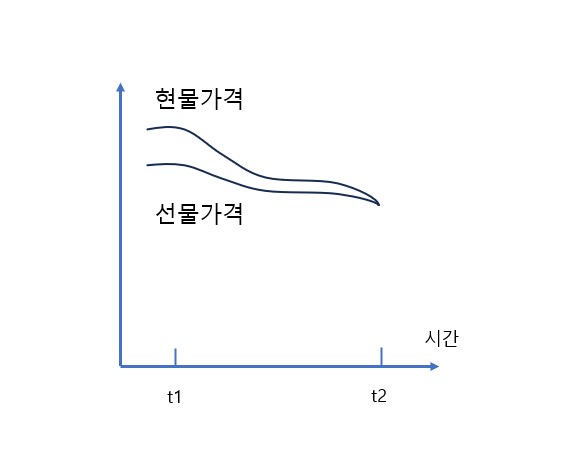 |
헷징을 t1시점에서 시작하고 t2시점에서 종결하는 것으로 가정하자. 헷징을 시작한 시점에서 현물가격과 선물가격이 각각 2.50달러, 2.20달러이다. 그리고 헷징을 종결한 시점에서 현물가격과 선물가격이 각각=2.20, 1.90달러이다. 즉 S1=2.50, F1=2.2, S2=2.00, F2=1.90이다.
베이시스를 구하면 다음과 같다.
b1 = S1 - F1, b2 = S2 - F2
즉, b1=0.30이고 b2=0.10이다.
먼저 헷저가 자산을 t2시점에서 매도할 것을 미리 알고, t1시점에서 선물계약에 매도포지션을 취한다고 하자. 자산의 판매가격이 S2이고 선물포지션으로부터 얻는 이익이 F – F2이다. 따라서 헷징전략과 자산매도를 통해 이룬 유효가격(effective price)은 다음과 같다.
S2 + F1 – F2 = F1 + b2
위의 예에서 유효가격은 2.30달러이다. F1의 값은 t1시점에서 알 수 있다. 만일 b2 또한 t1시점에서 알 수 있다면 완전헷지가 가능할 것이다. 헷징위험은 b2와 관련해서 발생하는 불확실성을 의미하고 이를 베이시스위험이라 부른다. 예를 들어 어떤 기업이 t2시점에서 자산을 구입할 예정이고 t1시점에서 매입헷지를 하려고 한다고 하자. t2시점에서 자산의 가격이 S2이고 매입헷지의 손실은 F1-F2이다. 따라서 헷지전략을 이용한 유효가격은 다음과 같다.
S2 + F1 – F2 = F1 + b2
이는 앞에서 설명한 것과 동일한 식이고 유효가격은 앞에서와 같이 2.30달러이다. F1의 값은 t1시점에서 수 있고. b2가 베이시스위험이다.
베이시스위험은 헷저의 포지션을 향상할 수도 있고 악화할 수도 있다. 매도헷지를 예로 들어보자. 만일 베이시스가 증가(strengthen)하면, 헷저의 포지션은 향상된다. 반면에 베이시스가 감소(weaken)하면 헷저의 포지션은 악화된다. 매입헷지에서는 매도헷지와 반대의 상황이 발생한다. 즉, 만일 베이시스가 증가하면 헷저의 포지션은 악화되는 반편에 베이시스가 감소하면 헷저의 포지션은 향상된다.
헷징 대상자산과 헷징선물의 기초자산이 다른 경우도 때때로 있다. 이를 교차헷징(cross hedging)이라고 한다. 교차헷징은 베이시스위험을 증가시킨다. S*2를 t2시점에서의 기초자산가격이라고 하자. 물론 S2는 헷징 대상자산의 t2시점에서의 가격이다. 헷징으로 기업이 지급하는(또는 받는) 금액은 다음과 같다.
S2 + F1 - F2
또는
F1 + (S*2 – F2) + (S2 - S*2)
S*2-F2와 S2-S*2는 베이시스의 두 구성요소이다. S*2-F2는 헷징 대상자산이 선물계약의 기초자산과 동일할 때의 베이시스이다. 그리고 S2-S*2는 두 자산 간의 차이로부터 비롯되는 베이시스이다.
17.2 계약의 선택
어떤 선물을 헷징에 이용할 것인지는 베이시스위험에 중요한 영향을 미친다. 선물계약의 선택은 다음 2가지 측면에서 고려되어야 한다.
1. 선물계약 기초자산의 선택
2. 인도월의 선택
만일 헷징 대상자산이 선물계약의 기초자산과 정확히 일치한다면, 첫 번째 선택은 일반적으로 쉽게 이루어진다. 그러나 일치하지 않는 경우에 헷징 대상자산과 가격 면에서 가장 밀접한 관련성을 갖는 선물을 선택하기 위하여 각별한 분석이 필요하다.
인도월의 선택은 여러 요인에 의해 영향을 받는다. 본 장의 앞의 예에서, 우리는 헷징의 만기가 인도윌과 일치하는 계약이 선택된다고 가정했다. 사실 더 늦은 인도월을 갖는 선물계약이 선택되는 것이 보통이다. 왜냐하면 선물가격이 인도월 동안 많이 변동되기도 하고, 만약 매입헷저가 인도월 동안 계속 계약을 유지한다면 현물자산을 인도받을 위험을 감수해야 하기 때문이다. 현물자산을 인도받는 것은 비용이 많이 들고 불편하다. 일반적으로 매입헷저들은 선물계약을 마감하고 보통의 공급자들로부터 현물자산을 매입하려고 한다.
일반적으로 베이시스위험은 헷징만기와 인도월 간의 차이가 증가할수록 커진다. 그러므로 인도월을 선택하는 가장 좋은 방법은 가능한 한 헷징만기보다 늦으면서도 근접한 인도월을 선택하는 것이다. 어떤 선물계약에 대해서 인도월이 3월, 6월, 9월, 12월의 4종류가 있다고 하자. 12월, 1월, 2월이 헷징만기인 경우 3월 만기의 선물계약이 선택될 것이고 3월, 4월, 5월이 헷징만기인 경우에는 6월 만기의 선물계약이 선택될 것이다. 이러한 원칙을 이용하는 데는 모든 선물계약이 충분한 유동성을 갖고 있다는 가정이 필요하다. 실제로 유동성은 만기가 짧은 계약일수록 커지는 경향이 있다. 따라서 헷저는 만기가 짧은 선물계약을 이용해서 계속 헷지 하는 방법(roll forward)을 사용하기도 한다.
17.3. 교차헷징
교차헷징(cross hedging)은 두 자산이 서로 다른 경우이다. 예를 들어 어떤 항공사가 제트연료의 미래가격이 상승할 것을 우려한다고 하자. 제트연료에 대한 선물계약이 없으므로 노출된 위험을 헷지하기 위하여 난방유 선물계약을 이용할 수 있다.
헷지비율(hedge ratio)은 위험노출 규모에 대한 선물포지션 규모의 비율이다. 선물계약의 기초자산과 헷지대상자산이 동일할 때 1.0의 헷지비율을 자연스럽게 이용한다. 지금까지의 예에서 사용한 혜지비율은 1.0이었다. 교차헷징의 경우 헷지비율을 1.0으로 하는 것이 항상 최적이지는 않다. 헷저는 헷지 되는 포지션 가치의 분산을 최소화시키는 헷지비율을 선택해야 한다. 헷저가 이 일을 어떻게 하는지 살펴보자.
17.4 최소분산 헷지비율의 측정
최소분산 헷지비율(minimum variance hedge ratio)은 현물가격의 변동과 가격의 변동 간의 관계에 기초하여 정해진다. 아래와 같은 기호를 이용하어 최소분산 헷지비율(최적 헷지비율)을 설명해 보기로 하자.
∆F : 헷지기간과 일치하는 기간 동안의 선물가격의 F의 변화
σS : ∆S의 표준편차
σF : ∆F의 표준편차
ρ : ∆S와 ∆F의 상관계수
h* : 최소분사 헷지비율(최적 헷지비율)
최소분산 헷지비율(optimal hedge ratio) h*는 [그림 17.2]에 나타난 것처럼 ∆S를 ∆F에 대해 회귀분석하여 얻은 회귀직선의 기울기이다. 이것은 직관적으로 쉽게 이해할 수 있다. h*는 F의 특정 변화에 대한 S의 평균변화의 비율이다. 최적 헷지비율(optimal hedge ratio) h*를 식으로 나타내면 다음과 같다.
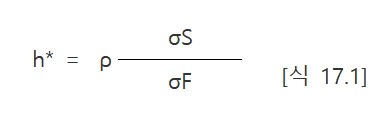
[식 17.1]에서 보듯이 최적 헷지비율 h* ∆S와 ∆F 사이의 상관계수와 ∆F의 표준편차에 대한 ∆S의 표준편차의 비율을 곱하여 구한다. [그림 17.2]은 헷저 포지션 가치의 분산이 선택된 헷지비율에 따라 어떻게 달라지는지를 보여주고 있다.
| 그림 17.2 선물가격 변화에 대한 현물가격 변화의 회귀분석 |
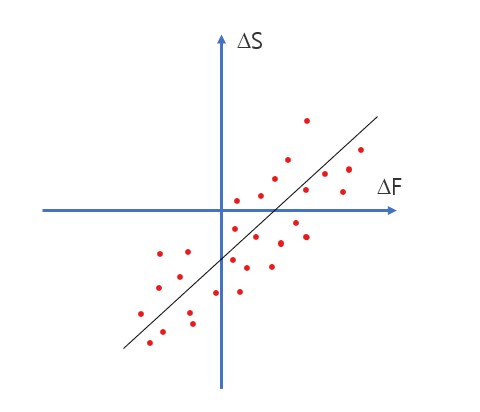 |
만약에 ρ=1이고 σF=σS이면, 최적 헷지비율 h* 는 1.0이다. 이런 결과는 예상된 것이다. 왜냐하면 이 경우 선물가격의 변동은 현물가격의 변동을 완벽하게 모방(mirror)하기 때문이다. 만약 ρ=1이고 σF=2σS이면, 최적 헷지비율 h*는 0.5이다. 이린 결과 역시 예상한 대로이다. 왜냐하면 이 경우 선물가격이 항상 현물가격의 2배만큼 변하기 때문이다. 헷지효과성(hedge effectiveness)은 전체분산에 대한 헷징에 의해 감소되는 분산의 비율로 정의된다. 헷지효과성은 ∆F에 대한 ∆S의 회귀분석에서 R²로 나타나는데 이는 곧 ρ²이 된다.
| 그림 17.3 헷지비율에 따라 변하는 헷저포지션의 분산 |
 |
[식 17.1]에서 변수 ρ, σF와 σS는 일반적으로 ∆S와 ∆F의 과거자료를 얻는다. 이상적으로 한 기간의 길이는 헷지 유효기간의 길이와 동일하여야 한다. 이와 같은 사실이 이용 가능한 관찰대상을 상당히 제한하기 때문에 실제로는 보다 짧은 기간이 이용된다.
17.5 최적 선물계약수
아래와 같은 기호를 사용하여 최적 선물계약수를 설명해 보기로 하자.
𝝔A : 헷지되는 포지션의 크기(수량)
𝝔F : 선물 1계약의 크기(수량)
N* : 최적헷징을 위한 선물계약의 수(최적 선물계약수)
헷징에 이용되는 선물계약은 h*𝝔A이다. 따라서 최적헷징을 위한 선물계약 수 N*는 다음과 같다.
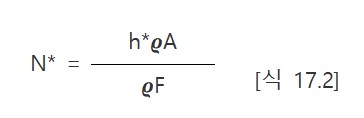
| 실무예제 17.1 | ||||||
어떤 항공사가 1개월 후에 2백만 갤런의 제트연료를 구입할 예정이며 헷징을 위해서 난방유 선물계약을 이용하려고 한다. 공식을 사용하여 표준편차와 상관계수를 구하면 σF=0.0313, σS=0.0263 그리고 ρ=0.928이다. 이들 값들을 [식 17.1]에 대입하여 계산하면 최소분산 헷지비율 h*는 0.7777이다. NYMEX에서 거래되는 난방유 선물의 1단위는 42,000갤론이다. [식 17.2]로부터, 최적선물계약수는 37.03임을 알수 있다. 0.928 × 0.0263 / 0.0313 = 0.7777 NYMEX에서 거래되는 난방유 선물의 1단위는 42,000갤론이다. [식 17.2]로부터, 최적선물계약수는 37.03임을 알수 있다. 즉, 반올림하면 최적 선물계약수는 37계약이 된다. 0.7777 × 2,000,000 / 42,000 = 37.03 즉, 반올림하면 최적 선물계약수는 37계약이 된다. |
17.6 헷지계약수의 조정
헷징을 위해 선물이 사용될 때, 헷지계약수의 조정(tailing the hedge)이라 불리는 약간의 조정이 필요한데, 이는 일일정산의 영향을 조정하는 것이다. 이는 실무적으로 [식17.2]가 다음과 같은 [식 17.3]으로 되는 것을 의미한다.

여기서 𝐕A는 헷지되는 포지션의 가치를 의미하고, 𝐕F는 선물 1 계약의 가치(=선물가격×𝝔F)를 의미한다. [실무예제 17.1]에서 갤런당 현물가격과 선물가격이 각각 1.94달러와 1.99달러라고 하자. 그러면 𝐕A=2,000,000×1.94=3,880,000달러이고, 𝐕F=42,000×1.99=83,580달러가 되어서, 결국 최적 선물계약수는 36.10 계약이 된다.
0.7777 × 3,880,000 / 83,580 = 36.10
만일 반올림하면 최적 선물계약수는 37계약이 아니라 36 계약이 된다. 헷지계약수 조정의 효과는 [식 17.2]의 헷지비율에 선물가격에 대한 현물가격의 비율을 곱한 것이 된다. 이론적으로 볼 때 헷징에 사용되는 선물포지션의 수는 현물가격과 현물가격의 변화를 반영하여 조정되어야 한다. 그러나 실제로는 조정하더라도 일반적으로 거의 차이가 없다. 만일 선물계약이 아니라 선도계약이 사용된다면, 일일정산을 하지 않기 때문에 [식 17.2]가 사용되어야 할 것이다.
[붙임]
이것은 일반적인 정의이다. 그러나 베이시스를 다음과 같이 정의하기도 한다. 베이시스=선물가격-현물가격 이는 금융선물에서 많이 사용하는 베이시스 정의이다.
'선물옵션투자이론' 카테고리의 다른 글
| 19. 헷지의 연장 (0) | 2023.11.25 |
|---|---|
| 18. 주가지수선물 (1) | 2023.11.24 |
| 16. 헷징에 대한 논쟁 (0) | 2023.11.21 |
| 15. 선물을 이용한 헷징전략 (0) | 2023.11.20 |
| 14. 선도계약과 선물계약의 비교 (0) | 2023.11.20 |



