주가지수선물에 대해 설명하고 주가지수선물이 주식투자 위험을 헷지 또는 관리하는 데 어떻게 이용되는지를 알아보기로 하자.
주가지수(stock index)는 구성 포트폴리오의 가치가 변함에 따라 변한다. 특정 시점에서 포트폴리오 내의 한 주식의 가중치는 그때에 그 주식이 포트폴리오 내에서 차지하는 투자비중과 동일하다. 주가지수가치의 증가율은 같은 기간 포트폴리오를 구성하는 주식들의 총 가치 증가율과 동일하다. 지수가 포트폴리오 투자로부터 얻는 자본이득과 손실을 추적하도록 하기 위하여 배당은 일반적으로 계산에 포함되지 않는다. [붙임 1] 참조
주식 포트폴리오가 고정되어 있더라도, 개별주식의 투자가중치는 고정되어 있지 않다. 포트폴리오를 구성하는 한 주식의 가격이 다른 주식들보다 급격히 상승한다면, 그 주식의 가중치는 자동적으로 커진다. 때때로 어떤 주가지수들은 수많은 주식 1주씩만으로 구성된 포트폴리오를 기초로 만들어진다. 이 경우에 배정된 가중치는 시장가격에 비례하고 주식분할 시에는 가중치가 조정된다. 다른 주가지수는 시가총액(=주가×발행주식수)에 비례해서 가중치가 부여된다. 시가총액을 기준으로 하면 주식분할, 주식배당 그리고 신주발행(new equity issue) 등에 대한 조정이 자동적으로 이루어진다.
18.1 주가지수
다우존스 산업평균지수(Dow jones Industrial Average)는 미국의 30개의 블루칩 주식들로 구성된 포트폴리오를 기초로 만들어진다. 주식의 투자가중치는 시장가격에 비례한다. CME 그룹은 다우존스지수에 대해 두 종류의 선물계약을 거래한다. 하나는 지수x10달러이다. 다른 하나(Mini 다우존스 선물계약)는 지수x5달러이다.
S&P 500 지수(Standard & Poor's 500 index)는 500개의 서로 다른 주식들로 구성되어 있다. 즉, 400개의 제조기업 주식, 40개의 공익기업(utilities) 주식, 20개의 운송기업 주식 그리고 40개의 금융기업 주식들로 구성되어 있다. 각 주식의 가중치는 일정시점에서 그 주식의 시가총액(=주가 발행주식수)을 기준으로 부여한다. S&P 500 지수는 뉴욕증권거래소에 상장된 모든 주식 시가총액의 약 80%를 반영하고 있다. 시카고상업거래소는 S&P 500 지수에 대하여 두 종류의 선물계약을 거래한다. 하나는 지수×250달러를 기준으로 하는 선물계약이고, 다른 하나(Mini S&P 500 선물계약)는 지수x50달러를 기준으로 하는 선물계약이다.
Nasdaq 100 지수는 나스닥 서비스를 이용하는 100개의 주식들을 기초로 만들어진다. CME 그룹은 두 종류의 선물계약을 거래한다. 하나는 지수x100달러를 기준으로 하는 선물계약이고, 다른 하나(Mini Nasdaq 100 선물계약)는 지수x20달러를 기준으로 하는 선물계약이다.
Russell 1,000 지수는 1,000개의 미국 대형주들을 기초로 만들어진 주가지수이다. U.S. dollar 지수는 6개의 외국통화(유로, 엔, 파운드, 캐나다 달러, 스웨덴 크로나 그리고 스위스 프랑)의 가치를 기초로 만들어진 지수이다.
앞의 [11.2]에서 언급한 바와 같이 주가지수 신물계약(futures contracts on stock indices)은 기초자산을 인도하지 않고 현금으로 정산된다. 모든 주가지수 선물계약들은 최종거래일에 지수의 시가 또는 종가로 정산된 후 마감된다. 예를 들어 S&P 500에 대한 선물계약은 인도월의 세 번째 금요일의 S&P 500 지수 시가로 종료된다.
18.2 주식 포트폴리오의 헷징
주가지수선물은 주식 포트폴리오를 헷지 하는 데 이용될 수 있다. 설명을 위해서 다음과 같이 정의하자.
VA : 포트폴리오의 현재가치
VF :주가지수선물 1 계약의 기초가 되는 주식들의 현재가치(현물지수 × 계약크기)
만약에 포트폴리오가 주가지수를 모방(mirror)한다면, 최적 헷지비울(h*)은 1이고 [식 18.1]에 따르면 매도되어야 할 선물계약수는 다음과 같다.
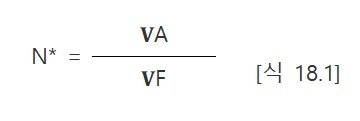
예를 들어 505만 달러의 포트폴리오가 S&P500을 모방한다고 하자. 주가지수의 현재가치가 1,010이고 선물 1 계약의 가치는 주가지수x250달러이다. 즉, VA=5,050,000이고, VF=1,010x250=252,500달러이므로 헷지를 위해서는 20개의 선물계약이 매도되어야 한다.
포트폴리오가 주가지수를 정확히 모방하지 않을 때에는, 적절한 헷지비율을 결정하기 위해서 CAPM의 베타(β)를 이용할 수 있다. 베타는 무위험수익률을 초과하는 포트폴리오수익률을 시장초과수익률에 대해 회귀분석 한 회귀직선의 기울기이다. 포트폴리오의 β가 1.0일 때 그 포트폴리오의 기대수익률은 시장수익률과 동일하고, β가 2.0일 때 그 포트폴리오의 초과수익률은 시장초과수익률의 2배이다. 물론 포트폴리오의 β가 0.5일 때 그 포트폴리오의 초과수익률은 시장초과수익률의 1/2이다.
β가 2.0인 포트폴리오는 ß가 1.0인 포트폴리오보다 시장변동에 대해서 2배의 민감도를 갖는다. 그러므로 β가 2.0인 포트폴리오를 헷지 하기 위해서는 2배의 선물계약이 필요하다. 마찬가지로 β가 0.5인 포트폴리오는 β가 1.0인 포트폴리오보다 시장변동에 대해서 0.5배의 민감도를 갖는다. 따라서 β가 0.5인 포트폴리오를 헷지 하기 위해서는 0.5배의 선물계약이 필요하다. 일반적으로 최적 선물계약수는 다음과 같다.

[식 18.2] 이 공식에서는 선물계약의 만기가 헷지기간과 거의 같다고 가정한다.
[식 18.2]를 [식 18.1]과 비교해 보면, h*=β임을 알게 된다. 이는 놀라운 일이 아니다. 최적헷지비율은 주가지수선물 가격 변화에 대해 회귀분석 한 포트폴리오가격 변화의 기울기이다. 베타(β)는 주가지수수익률에 대해 회귀분석 한 포트폴리오수익률의 기울기이다. 이 공식을 이용하는 예를 들어 보기로 하자. 즉, 만기가 4개월 후인 선물계약을 이용하여 3개월 동안 어떤 포트폴리오의 가치를 헷지 하려는 상황을 고려해 보자.
S&P 500 지수 = 1,000
S&P 500 지수 선물가격 =1,010
포트폴리오의 가치 = 5,050,000달러
무위험이자율= 연 4%
&P 500의 배당수익률 = 연 1%
포트폴리오의 베타 = 1.5
선물 1 계약의 크기는 지수×250달러이다. 즉, VF=250x1,010=252,500달러이다. [식 18.2]를 이용하여 포트폴리오를 헷지 하기 위해 매도해야 하는 선물의 최적계약수를 구하면 다음과 같다.
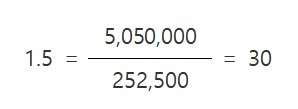
지수가 3개월 후 900이고, 선물가격이 902달러라고 하자. 그러면 선물 매도포지션으로부터 얻는 이익은 810,000달러이다.
30 x (1010- 902) x 250 = 810,000달러
지수하락에 따른 손실이 10%이고, 지수에는 연간 1%, 즉 3개월마다 0.25%의 배당이 포함된다. 배당을 감안하면 지수투자자는 3개월에 9.75%의 손실을 보는 셈이 된다. 포트폴리오의 베타가 1.5이므로 CAPM에 따르면 다음 식이 성립한다.
포트폴리오 기대수익률 - 무위험수익률 = 1.5 x (지수수익률 - 무위험수익률)
이를 이용하여 계산하면 포트폴리오의 기대수익률은 –15.125%이다.
1.0 + [1.5 x (-9.75 – 1.0)] = -15.125
3개월 후의 포트폴리오의 기대가치(배당포함)는 다음과 같다.
5,050,000달러 x (1 - 0.15125) = 4,286,187달러
헷징이익을 포함한 헷저포지션의 기대가치는 다음과 같다.
4,286,187달러 + 810,000달러 = 5,096,187달러
[표 18.1]는 만기 시의 주가지수에 따라 지수선물가격, 선물포지션의 이익 등이 어떻게 되는지를 보여주는 표이다. 이 표로부터 3개월 후의 헷저포지션의 총가치는 지수가치와 거의 독립적임을 알 수 있다.
여기서 우리가 감안하지 못한 한 가지는 선물가격과 현물가격 간의 관계이다. 현재 선물가격으로 가정한 1,010은 주어진 이자율과 배당수익률 하에서 대략적으로 기대되는 가격이라는 것을 알게 될 것이다. 또한 [표 18.1]에 제시된 3개월 후의 선물가격의 경우에도 그러하다. [붙임 2] 참조
| 표 18.1 주가지수 헷징의 성과 | |||||
| 3개월 후 지수가치 |
900 | 950 | 1,000 | 1,050 | 1,100 |
| 현재 지수선물가격 |
1,010 | 1,010 | 1,010 | 1,010 | 1,010 |
| 3개월 후 지수선물가격 |
902 | 952 | 1,003 | 1,053 | 1,103 |
| 선물포지션으로부터의 이익(달러) |
810,000 | 435,000 | 52,500 | -322,500 | -697,500 |
| 시장수익률 |
-9.750% | -4,750% | 0.250% | 5.250% | 10.250% |
| 포트폴리오수익률 |
-15.125% | -7.625% | -0.125% | 7.375% | 14.875% |
| 3개월 후 포트폴리오 (배당포함)의 가치(달러) |
4,286,187 | 4,664,937 | 5,043,687 | 5,422,437 | 5,801,187 |
| 3개월 후 포지션의 총가치(달러) |
5,096,187 | 5,099,937 | 5,096,187 | 5,099,937 | 5,103,687 |
18.3 주식 포트폴리오를 헷지 하는 이유
[표 18.1]에 따르면 3개월 후에 헷저포지션의 가치는 헷징전략 실시 전보다 1% 정도 높다. 이는 놀라만 한 사실이 아니다. 무위험수익률이 연 4% 또는 분기당 1%이므로, 헷지결과 투자자의 포지션 가치가 무위험수익률 정도로 성장한 셈이다. 그렇다면 헷저가 많은 어려움에도 불구하고 왜 선물계약을 이용하는지에 대한 의문이 자연히 제기될 것이다. 만일 헷저의 목적이 무위험수익률만큼 수익을 얻는 것이라면, 간단히 포트플리오를 매도하고 그 대금을 단기국채에 투자하면 된다. 그럼에도 불구하고 헷징이 필요한 이유들 두 가지만 들어보면 다음과 같다.
첫째, 포트폴리오를 잘 구성했다고 느낀다면 헷징은 정당화될 수 있다. 이 경우 헷저는 전체 주식시장의 투자성과에 대해서는 매우 불확실해하지만 보유 포트폴리오가 시장보다 높은 수익률(베타 위험조정 후의 수익률 기준)을 올릴 것이라고 확신하고 있다. 이패 주가지수선물을 이용하여 헷지 하면, 포트폴리오를 보유화면서 부담하는 시장위험이 제거된다. 따라서 헷저는 시장보다 높은 수익률을 얻을 수 있는지에 대한 위험만 부담하게 된다.
둘째, 주식 포트폴리오를 장기간 보유할 예정인 투자자가 단기 시장위험으로부터 보호받기를 원할 때 헷징이 필요하다. 물론 헷징전략 이외에도 보유 포트폴리오를 매도하고 나중에 그것을 다시 매입하는 전략을 이용할 수도 있으나, 이 전략은 많은 거래비용을 발생시킬 수 있다.
18.4 포트폴리오 베타의 변화
[표 3.4)의 예에서 헷저가 보유하는 포트폴리오의 베타는 0으로 줄어들어서 헷저의 기대수익률은 주가지수의 성과와 거의 독립적이다. 선물은 포트폴리오의 베타를 0 이외의 값으로 변화시키는 데에도 이용된다. 앞의 예를 계속해서 사용하여 설명하기로 하자.
S&P 500 지수= 1,000
S&P 500 지수 선물가격= 1,010
포트끌리오의 가치 = 5,050,000달러
무위험이자율 = 연 4%
포트폴리오의 베타 = 1.5
선물 1 계약의 가격은 지수x250달러이므로 𝐕F=252,500달러이다. [식 18.2]에 따르면 포트폴리오의 위험을 완전히 헷지 하기 위해서 지수선물 30 계약을 매도해야 한다.
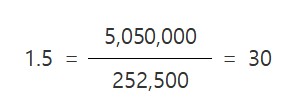
포트폴리오의 베타를 1.5에서 0.75로 감소시키기 위해서는 매도선물 계약의 수가 앞에서 구한 30 계약이 아니라 15 계약이어야 한다. 그리고 베타를 2.0으로 증가시키기 위해서는 10개의 선물계약에 매입포지션을 취하여야 한다. β > β*일 때, 포트폴리오의 베타를 β에서 β*로 감소시키기 위해 요구되는 매도선물포지션의 수는 다음과 같다.
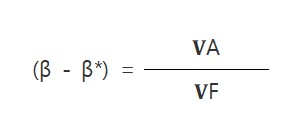
그리고 β > β*일 때, 포트폴리오의 베타를 β에서 β*로 증가시키기 위해 요구되는 매입선물포지션의 수는 다음과 같다.

18.5 주식 선택 능력의 편익을 누리는 방법
본인 스스로를 시장보다는 성과를 더 올릴 수 있는 투자자라고 생각한다고 하자. 당신은 향후 몇 개월 동안 시장이 어면 성과를 낼지 모르지만, 당신의 포트폴리오가 시장보다 성과를 더 낼 것을 자신한다. 당신은 어떤 행동을 취해야 하는가?
당신은 주가지수선물을 β𝐕A / 𝐕F 만큼 매도해야 한다. 여기서 β는 보유 포트폴리오의 베타이고, 𝐕A는 보유 포트폴리오의 총가치이며, 𝐕F는 주가지수선물 1 계약의 현재가치이다. 만일 당신이 보유한 포트폴리오가 동일한 베타를 갖는 잘 분산된 포트폴리오보다 성과를 더 낸다면 당신은 돈을 벌 것이다.
예를 들어 4월 현재 주가가 100달러인 IBM 주식 20,000주를 소유한 투자자가 있다고 가정해 보자. 투자자는 다음 달에 시장이 크게 변동할 것으로 판단하고 있다. 그러나 그는 IBM 주식의 수익률이 시장수익률보다 우월할 것이라고 믿고 있다. 투자자는 세 달 동안 시장의 수익률을 헷지 하기 위해 8월 만기 S&P 500 지수 선물을 이용하기로 한다. IBM 보통주의 베타는 1.1이다. 8월 만기 S&P 500 지수 선물의 가격이 900이고, 지수선물 1 계약은 지수×250달러이다. 즉, 이 경우에 𝐕A=20,000x100=2,000,000달러이고, 𝐕F는 900x250=225,000달러이다. 따라서 매도해야 한 선물의 최적 계약수는 다음과 같다.

반올림하면 헷저는 한 달 후 포지션을 마감할 예정으로 선물을 10 계약 매도한다. IBM 주가가 한 달 동안에 90달러로 하락하고 S&P 500 지수가 750으로 하락한다고 하자. 투자자가 선물계약에서 10x250달러(900-750)=375,000 달러를 이익 보는 반면, IBM 주식투자에서는 20,000x(100달러-90달러)=200,000달러의 손실을 본다. 이 예에서 투자자의 총이익은 175,000달러이다. 왜냐하면 IBM의 주가는 1.1의 베타를 갖는 잘 분산된 포트폴리오만큼 하락하지 않기 때문이다. 만일 시장이 상승하고 IBM의 주가가 1.1의 베타를 갖는 잘 분산된 포트폴리오보다 더 상승한다면(투자자가 그령게 기대했듯이), 이 경우에도 역시 투자자는 전체적으로 이익을 볼 것이다.
[붙임 1]
이에 대한 예외로 총투자수익률지수(total return index)가 있다. 이 지수는 포트플리오로부터 얻는 배당이 포트폴리오에 재투자된다고 가정하여 계산된다.
[붙임 2]
[표 18.1]는 지수에 대한 배당수익률이 예측 가능하고, 무위험수익률이 일정하고 3개월 간의 지수수익률이 포트폴리오의 수익률과 완전한 상관관계를 갖는다고 가정하고 계산된 것이다. 실제로는 이런 가정이 완전히 지켜질 수는 없고 실제 헷징성과는 [표 18.1]에서 보인 헷징성과보다 못하다.
'선물옵션투자이론' 카테고리의 다른 글
| 20. 자본자산 가격결정 모형(CAPM) (0) | 2023.11.27 |
|---|---|
| 19. 헷지의 연장 (0) | 2023.11.25 |
| 17. 베이시스위험 (0) | 2023.11.22 |
| 16. 헷징에 대한 논쟁 (0) | 2023.11.21 |
| 15. 선물을 이용한 헷징전략 (0) | 2023.11.20 |



